ユークリッド幾何の第1公準

この記事は、日曜数学アドベントカレンダーの2日目の記事です。
adventar.org
1日目はtsujimotterさんの「パスカルの三角形にたくさん出てくる数: 3003」でした。3003はパスカルの三角形に何回出てくるのでしょうか？追記された部分も面白いのでまだ読んでいない方はぜひ読んでみてください。
tsujimotter.hatenablog.com

---

2日目のテーマはユークリッド幾何の第1公準です。

ユークリッドの『原論』といえば平行線の公理とも呼ばれる第5公準をめぐる物語でしょう。

第5公準 １本の線分が２本の線分と交わり, 同じ側の内部に作る角の和が２直角より小さいとき, これら２本の線分を延長すると, 角の和が二直角より小さい側で交わる

この第5公準を言い換えた次のものを平行線の公理と呼ぶことも多いようです。

第5公準の言い換え 与えられた直線外の1点を通り，この直線に平行な直線がただ1本存在する

他にも「三角形の内角の和が2直角（180°）」とも言い換えられることが知られています。

平行線公準 - Wikipedia

この第5公準は他の公準とくらべて文章が長く複雑なので，本当に幾何の基礎たる公準に入れる必要があるのか，多くの人が疑問に思いました。そして，多くの数学者が第5公準を第1公準から第4公準を使って証明できないかと挑戦してきました。そのような試みから始まり，双曲幾何の発見により第5公準の独立性（第1～第4公準から証明も反証もできないこと）が証明されるまでの物語は，2000年を超える壮大なものです。

今日はこの平行線の公理ではなくて，第1公準について色々と考えてみましょう。

第1公準 与えられた２点を結ぶ線分を1本だけ引くことができる

単に2点を定木を使ってピッと結べば線分の出来上がり。第5公準にくらべると「当たり前」で，証明の必要のない事実として受け入れることに抵抗はないでしょう。

いつもみんなの笑いもの，ってことはないですが，個別に扱うにはツマラナイものに思えるかもしれません。ところが考察してみるとなかなかどうして色々と面白い話が出てきます。

ちなみに内容は独自研究みたいなものですので，他所の解説記事とは異なることも書いてあると思います（いろいろ調べてみると第1～第5公準のそれぞれが本当に何を意味しているのか世間の合意が取れていないようにも思えます。しかし「○○かどうかは公準の解釈による」とか言っていたら何も考えられないので，この記事は「ユークリッド原論の記述をそのまま素直に読む」という立場で書いています）。正直，手を出すのがちょっと怖いネタですね。あくまで一説として読んで下さい。何か思うことがあればコメントをくれるとありがたいです。

Contents

ユークリッド原論の５つの公準

実は『原論』は原典が現存しておらず写本しか残っていません。全13巻ある『原論』の第1巻では点・直線・円・直角などの定義から始まり，5つの公準と9つの公理が提示され，平面幾何に関する48個の命題が証明されています。

この記事では，平面幾何に関わる5つの公準を以下の通りとします。

第1公準 与えられた２点を結ぶ線分を1本だけ引くことができる
第2公準 与えられた線分を延長することができる
第3公準 与えられた点と半径で円を描くことができる
第4公準 すべての直角は等しい
第5公準 １本の線分が２本の線分と交わり, 同じ側の内部に作る角の和が２直角より小さいとき, これら２本の線分を延長すると, 角の和が二直角より小さい側で交わる

こっそり修正されている 第1 公準

実はこの第1公準はオリジナルのものとちょっと異なります。Wikipediaから引用すると
ユークリッド原論 - Wikipedia

任意の一点から他の一点に対して直線を引くこと

とあり，「1本だけ」という条件が入っていません（ここでいう「直線」とは，現代でいう「線分」のことです）。この条件は9番目の公理から導かれます。再びWikipediaから引用します。

1. 同じものに等しいものは、互いに等しい
（中略）
9. [2線分は面積を囲まない］
ただし［］で囲まれた公理は公理に含めないことがある。

2線分が面積を囲むとは，例えば次の図のようになることです。

つまり2点 を結ぶ線分が2本以上ある場合です。

そこで，「与えられた２点を結ぶ線分を1本だけ引くことができる」としたものを新たに第1公準として採用することにします。

「公準」と「公理」をそれぞれ見てみると，公準は幾何に関するもの，公理は一般的な等式・不等式に関わるものになっていますが，なぜかこの9番目の公理だけは幾何に関するものになっています。しかも公理に含めたり含めなかったりするとの注釈が入っており，いろいろと謎が残ります。

憶測ですが，後世の人が写本を作る際に必要と思って付け加えようとしたのだけれど，神聖な5つの公準はいじることが出来ずに仕方なく公理の最後にくっつけたのかもしれません。

ユークリッド幾何のスーパースター「平行線の公理」

今回の話の本題ではないですが，第5公準に触れないわけにはいかないでしょう。

第5公準 １本の線分が２本の線分と交わり, 同じ側の内部に作る角の和が２直角より小さいとき, これら２本の線分を延長すると, 角の和が二直角より小さい側で交わる

この第5公準は「与えられた直線外の1点を通り，この直線に平行な直線がただ1本存在する」「三角形の内角の和が2直角（180°）」とも言い換えられることが知られています。

多くの数学者が第5公準を第1～第4公準を使って証明できないかと挑戦してきました。そして双曲幾何の発見により，第5公準を第1～第4公準から証明できないことが分かることになるのですが，その答えを知った後にこの「第5公準を証明せよ」という問題を見直してみると，この問題は二重の意味で「解くのが不可能な問題」であることが分かります。

• 第5公準は第1～第4公準から証明できない
• そして「第5公準は第1～第4公準から証明できない」こともユークリッド幾何の内部では証明できない

という2つの大きな壁が問題解決の前に立ちふさがっていたのです。

これは「幾何学といえばユークリッド幾何」が常識の時代に気付くことは不可能と言ってもいいでしょう。まさに数学者の人生を食いつぶす「悪魔の問題」です。

第5公準の独立性は，問題が解決された今日でも初学者はなかなか簡単に理解できるものではないと思います。それは双曲幾何のモデルをちゃんと理解するのが難しいからです。

そこで，ここでは第1公準の独立性について話をしましょう。第5公準の独立性を理解するときの練習にもなると思います。

球面幾何

ユークリッド幾何とは異なる公準を持つ幾何を非ユークリッド幾何と呼びます。双曲幾何も非ユークリッド幾何のひとつです。

ここではユークリッド幾何のひとつである球面幾何をいうものを紹介します。

図形を球面上で考える幾何学を球面幾何といいます。

球面上の点を「点」，球面に沿って２点を結ぶ最短の曲線を「線分」，球面上のある点から一定の距離にある点の集まりを「円」，２つの線分のなすの「角度」は線分の接線のなす角度と解釈します。

すると，「線分」は大円（球の中心を通る平面と球面との交わりでできる円）の一部になり，「円」は通常の意味での円と同じ図形になります。

「線分」をずっと延長したものが「直線」なので，大円が球面上の「直線」に当たります。なので，球面幾何では直線は特殊な円ということになります（ユークリッド幾何の直線も「半径が無限大の円」と解釈できなくもないですが）。

なぜ大円が球面上の「直線」となるのか，（ごまかした）説明をしてみます。

まず直感的に説明すると，大円は球面に描ける一番曲がりが“緩い”曲線です。つまり，球面上の曲線の中で一番普通の意味での直線っぽいものなので，点同士を最短に結ぶ曲線は大円の一部にります。

まあそんな気もするけどちょっと納得しづらいですかね？それでは“物理的に”説明してみましょう（もちろんごまかしの説明です）。

球面にへばりついて生活している「球面人」を考えてみましょう。球面人にとっては自分が住んでいる球面だけが世界の全てで，実は外の世界があって自分は球面に束縛されているだけである事を感じることが出来ないとします。さて，球面人がツルツルのソリに乗って大円上を一定の速度で滑っているとしましょう。外の世界にいる我々から見ると，球面人のソリは等速円運動をしているわけですから，大きさが一定で球の中心に向う向心力が作用している運動をしているように見えます。この向心力は，ソリを球面上に束縛するための力です。球面人は自分は球面に束縛されていることを感じられないので，この向心力を感じることが出来ません。つまり，球面人は自分には何の力もかかっていないと感じていることになります。物理には慣性の法則「外力が働かなければ，物体は静止または等速直線運動を永遠に続ける」というものがありました。球面人の世界でも慣性の法則が成り立つとすると，大円が「球面人にとっての直線」であるという結論になります。

球面幾何と5つの公準

これから球面幾何で第1公準～第5公準が成り立つか見てみましょう。

このときに注意するのが「書いてある通りに解釈する」ということです。公理系というのは厳密な論理のルールなので，書いてもいない内容を勝手に想像して読み込んでいたら，一体何が前提なのか分からなくなってしまいます。言われたことをそのままの意味にしか取れないカタブツAIロボになった気持ちで球面幾何で第1公準～第5公準が成り立つかをチェックしていきましょう。

球面幾何と第1公準

まずは第1公準からです。

第1公準 与えられた２点を結ぶ線分を1本だけ引くことができる

球面幾何では第1公準は成り立ちません。北極と南極を結ぶ「線分」が1本だけでなく，無数に存在するからです。

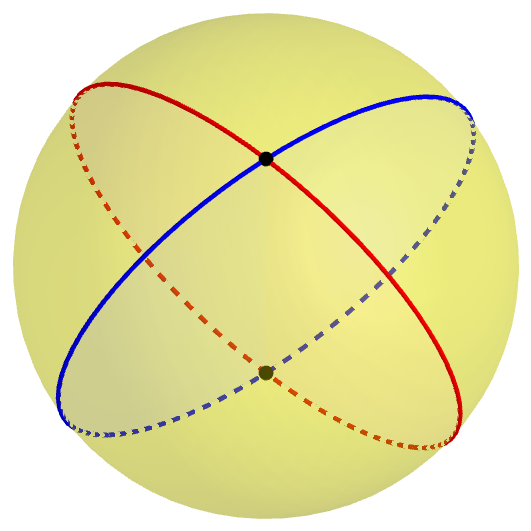
しかし，「2点を結ぶ線分が存在する」という命題は成り立ちます。成り立っていないのは，2点を結ぶ線分の一意性の部分だけです。こうしてみると，追加された「1本だけ」という条件がいかに大事かが分かります。

球面幾何と第2公準

第2公準について見てみましょう。

第2公準 与えられた線分を延長することができる

球面幾何での「直線」である大円は長さが有限で，ずっと延長していくと元の点に戻ってきてしまい，第2公準が成り立つとしていいか迷うかもしれません。また，球面幾何では線分を延長していくと線分でなくなってしまいます。

南極 から伸びる線分 の端点 を動かして線分を延長していくと， が北極 に到達するまでは円弧 は球面上の線分ですが，北極 を通り過ぎると円弧 は球面上の線分でなくなってしまいます（逆方向から繋いだ方が最短路）。

しかし，単に「線分を延長する」という操作はできているように見えます。

正直「延長することができる」の言葉の解釈の問題のような気もしますが*1「線分を延長して元の点に戻って来てはいけない」「線分を延長した結果も線分である」とはどこにも書いていないので（カタブツAIロボの精神）この記事では 球面幾何では第2公準は成り立っている と解釈することにします*2。

球面幾何と第3公準

第3公準について見てみましょう。

第3公準 与えられた点と半径で円を描くことができる

球面上の円には大きさの上限があります。つまり，あまりにも大きな半径を指定すると，その半径を持つ円を描くことができないので，球面幾何では第3公準は成り立たないと思ってしまうかもしれません。

しかし，この考え方は「半径」の定義を誤解しています。もしくは第3公準が成り立つかは「半径」の定義によると言ってもいいでしょう。ではどの定義を採用するかというと，ユークリッド原論の定義を採用するのが一番フェアでしょう。

ユークリッド原論の円の定義を引用してみましょう。定義の15番目が円の定義で，17番目が直径の定義です。
pisan-dub.jp

円とは周と呼ばれる一つの線の境界で囲まれた平面図形であって、その中にある一つの点から円周上の点に引かれた直線の長さがすべて等しいようなものである。
（中略）
直径とは、円の中心を通り、円周上に両端をもつ直線であり、それによって円は二分される。

ここでいう「直線」とは，現代でいう「線分」のことです。半径は直径の半分のことなので，この定義によれば「半径」の定義は「現代的な意味での実数」ではなくて「線分」であることが分かります。実際に原論の証明の中でも，円を描くときは中心と円が通る点を指定しています。

そもそもユークリッド原論では，長さ・角度・面積を数値で表して比較するということを一切しません 。というより，線分や三角形などの「図形」と長さや面積などの「量」を分けて考えるという思想がそもそも無いようです。

ロマンティック数学ナイトで日曜数学会キグロ氏が原論の魅力を語る - ログミーBiz

球面幾何で第3公準が成り立つかは，球面上のある点とそこから伸びる線分があったとき，その点を中心とし，その線分を半径とする円を描けるかどうか判定すればいいことになります。球面上ではそのような円は描くことができます。第3公準は球面幾何で成り立ちます。

球面幾何と第4公準

第4公準について見てみましょう。

第4公準 すべての直角は等しい

球面幾何では第4公準は成り立ちます。直角とは直線をその直線上の点で真っ二つに分けたもののことです。どの直角も↓と同じ形です。

疑いの余地なし！ありがとう第4公準！

球面幾何と第5公準

最後はスーパースター第5公準です。

球面上の「直線」は大円でしたが，球面上のどんな2つの大円も交わることはすぐに分かります。つまり，球面幾何には「平行線」というものは存在しません。

平行線の公理こと第5公準は「与えられた直線外の1点を通り，この直線に平行な直線がただ1本存在する」と言い換えられたので，平行線が存在しない球面幾何では第5公準は成立しない，としてしましそうですが，ここに大きな落とし穴があります。

「第5公準は『与えられた直線外の1点を通り，この直線に平行な直線がただ1本存在する』と言い換えられる」というのには大事な前提が抜けていて，正確に言うと「第1～第4公準が成立するという仮定のもとで，第5公準は『与えられた直線外の1点を通り，この直線に平行な直線がただ1本存在する』と言い換えられる」となります。球面幾何では第1公準が成り立たないので，実はこの言い換えはできません。

オリジナルの第5公準を見てみましょう。

第5公準 １本の線分が２本の線分と交わり, 同じ側の内部に作る角の和が２直角より小さいとき, これら２本の線分を延長すると, 角の和が二直角より小さい側で交わる

第5公準は，ある条件のもとで延長した2本の線分が交わることを主張する命題です。球面幾何では何の条件もなしに，線分を延長する方向に関わらず，どんな2本の線分も延長すると交わるので球面幾何では第5公準は成り立っているのです（命題「PならばQ」はQが真ならばPの真偽に関わらず真です）。

第1公準の独立性

以上より（この記事の解釈では）球面幾何では第1公準だけ成り立たず，第2～第5公準は成り立つことが分かりました。

この事から，第1公準は第2～第5公準から独立している（証明も反証もできない）ことが分かります。

第2～第5公準から第1公準が証明できると仮定すると，球面幾何では第2～第5公準が成り立っているので，球面幾何でも第1公準が成り立つことになりますが，実際には球面幾何では第1公準は成り立っていないので矛盾です。よって第2～第5公準から第1公準は証明できません。

また，第2～第5公準から「第１公準の否定」が証明できると仮定すると，ユークリッド幾何では第2～第5公準が成り立っているので，ユークリッド幾何でも「第１公準の否定」が成り立つことになりますが，実際にはユークリッド幾何では第1公準が成り立っているので矛盾です。よって第2～第5公準から「第１公準の否定」は証明できません。

つまり，第1公準は第2～第5公準から独立しています。

第1公準の独立性を教えてくれるのが5つの公準のうち第1公準だけを満たさない球面幾何でした。第5公準の独立性を証明したければ，5つの公準のうち第5公準だけを満たさない「幾何」を見つければいいことになります。それが今日では双曲幾何と呼ばれているものです。

三角形の内角の和

せっかく球面幾何を出したので，三角形の内角の和についても見てみましょう。

ユークリッド幾何では三角形の内角の和は2直角（180°）でした。原論では32番目の命題として証明されています。

三角形が与えられたとき，図のようにを延長し，に平行なを引きます。平行線に交わった直線の錯角・同位角がそれぞれ等しいので三角形の内角を1直線上に集めることができ，三角形の内角の和が180°になることが証明されます。

一方で球面幾何では，三角形の内角の和は180°より大きくなります。例えば，どの角も直角であるような三角形が存在します。

つまり，先ほどのユークリッド幾何における「三角形の内角の和は2直角（180°）」の証明をそのまま球面幾何も当てはめると。どこかで破綻することになります。どこで破綻しているか分かるでしょうか？

まず気付くのは球面幾何には平行線が存在しないのに，証明では平行線を引いているところですね。なのでこの証明は球面幾何では使えません。

サッケーリ・ルジャンドルの定理

ここからさらに三角形の内角の和の深い話に入りましょう。実は，第1公準～第4公準だけを使って「三角形の内角の和は2直角（180°）以下」であることが証明できます。この定理はサッケーリ・ルジャンドルの定理と呼ばれるものです。双曲幾何も第1公準～第4公準を満たすので，「三角形の内角の和は2直角（180°）以下」は双曲幾何でも成り立つことになります。

球面幾何ではサッケーリ・ルジャンドルの定理は成立しないので，やはりその証明は球面幾何では破綻することになります。その原因は球面幾何では第1公準が成り立たないことです。

逆に言うと，サッケーリ・ルジャンドルの定理には第1公準が本質的な役割を果たしているということになります。このことを見ていきましょう。

サッケーリ・ルジャンドルの定理の証明

サッケーリ・ルジャンドルの定理
第1公準～第4公準だけを使い，三角形の内角の和は２直角以下であることが証明できる。

サッケーリ・ルジャンドルの定理は原論の命題17を使って証明されます。また，命題17は命題16を使って証明されます。まずは命題16・17の証明をします（命題16は命題17の証明に必要な部分だけ証明します）。

命題16 三角形の外角はその隣り合わない内角よりも大きい。
命題17 三角形の内角2つの和は2直角より小さい。

（証明）

が与えられたとき，図のようにを延長し（第2公準）， の中点 を取り（命題10）， を結んだ線分（第1公準）を延長してとなる点を取り（第2公準），線分を引く（第1公準）。対頂角は等しいので （命題15）。よって， と は2辺とそのはさむ角がそれぞれ等しいので合同となり，特に （命題4）。よって外角 は内角 より大きい。これで命題16（の半分。隣り合わない内角はもう一個あるから。）は示された。

また， において は，2直角よりも だけ小さいので，命題17も示された。
（証明終）

命題16の証明には命題10や命題15を使っていますが，実はユークリッド原論では命題1～命題28は第5公準を一切使わずに証明されています。つまり命題17も第1公準～第4公準だけを使い証明でされていることになります。

命題10や15の証明は下記サイトで読むことができます。
ユークリッド原論 総目次

キグロさんのブログもおすすめです。
stoixeia.hatenablog.com

ちなみに，ここで証明した命題17は第5公準の逆になっています。

図で「 ならば が交わる」と主張するのが第5公準です。逆に が交わるとすると， が三角形をなすので， 命題17は「 が交わるならば 」という第5公準の逆を主張していることになります。

サッケーリ・ルジャンドルの定理を証明しましょう。

サッケーリ・ルジャンドルの定理
第1公準～第4公準だけを使い，三角形の内角の和は２直角以下であることが証明できる。

（証明）
背理法で証明する。内角の和が2直角より だけ大きい が存在したと仮定する。もし， のとき，命題16と同様の作図をする。

は内角の和が と等しい（どちらも●+●+●+●）。また， と は足すと の内角 と等しいので，どちらかは の半分より小さい。

そこで， と の小さい方を新たな として， を新たな とする。

以下同じ操作を繰り返すと， の内角の和は変わらず， の大きさは1回ごとに半分以下になっていく。よって有限回の操作で の内角の和は2直角より だけ大きく， という2つの性質を満たす に到達する*3。このとき， は2直角より大きくなるが，これは命題17に矛盾する。

よって，背理法により，三角形の内角の和が２直角を超える三角形は存在しないことが証明された。
（証明終）

サッケーリ・ルジャンドルの定理の証明はなぜ球面幾何で破綻するのか

球面幾何では三角形の内角の和が2直角を超えるので，サッケーリ・ルジャンドルの定理の証明をそのまま当てはめようとするとどこかで破綻します。

球面幾何で成り立たないのは第1公準の中でも，2点を結ぶ線分の一意性の部分だけなので，この一意性を使わないと証明がうまくいかない部分があるはずです。

それはどこでしょうか？

実は球面幾何では，命題16の時点で証明が破綻していることが分かります。先ほどのすべての角が直角の三角形を見てみましょう。

このとき，外角とその隣り合わない内角はどちらも直角で等しくなってしまっています。命題16は「三角形の外角はその隣り合わない内角よりも大きい」ことを主張していたので，球面幾何では命題16は成り立ちません。

では，このすべての角が直角の三角形に対して，命題16の証明はなぜうまくいかないのでしょうか？

命題16と全く同じ作図をこの三角形にしてみましょう。線分 の中点 を取り，線分 を延長して となる地点に点 を取ります。

すると点 が線分 を延長した直線上に来てしまいます。 と が合同で というのは正しいのですが， が外角の一部ではなく外角全体になってしまい，外角より真に小さいという事が成り立たなくなってしまっています*4。

つまり命題16の証明で点 を取るときに，

第1公準により2点を結ぶ線分は一意なので，線分 を延長しても を延長した直線と交わらない

というところに第1公準の2点を結ぶ線分の一意性が効いているのです*5。

命題16の証明を読んだときに，おそらくこのことを意識することはなかったと思います。

このように非ユークリッド幾何を考えることで，ユークリッド幾何の証明において各公準がどのような働きをしているか，より深く理解できるようにもなるのです。

おしまい。

---

明日は grand_antiprism さんの Asgeirsson's Mean Value Theorem の話です。
grandantiprism.hatenablog.com

---

*1:実際，ネットで調べた範囲でも球面幾何で第2公準が成り立つかは記事によってまちまちで，日本語版Wikipediaの楕円幾何学の項では球面幾何は楕円幾何の一部で楕円幾何では第2公準は「成り立たない」と言っているし，英語版Wikipedia の Spherical geometryでは「成り立つ」と言っています。実射影平面が標準的なモデルになるものが楕円幾何としている記事もあって，球面幾何が楕円幾何の一部かどうかも楕円幾何の定義によるようです。

*2:ただ，第2公準が「線分を延長しても元の点に戻ってこない」「線分を延長したものも線分になる」という内容を含んでいないとすると，気なる問題があることは確かです。それはこれらの命題がユークリッド幾何で成り立つことを保証しているものは何かという問題です。個人的にはこれは第2公準単独の問題にせずに，第1公準と，さらにヒルベルトが著書『幾何学基礎論』で導入した「順序の公理」を含めた議論にした方がいいと思います。長くなるのでこのことは別記事にしたいと思います。いまいち納得のできない方は，とりあえず「球面幾何で第2公準が成り立つという解釈もあるかなぁ」くらいで続きを読んでください。

*3:ここでアルキメデスの原理というものを使っています。ユークリッド原論ではアルキメデスの原理は当たり前のものとして扱われているようです。

*4:一方で を延長するところと， を延長した線上に点 を取るところで，第2公準「与えられた線分を延長することができる」はちゃんと球面上でも働いているように見えます。

*5:追記：日曜数学会の数学忘年会のニコ生タイムシフトを見て知ったのですが，このことはキグロさんの記事の追記にある通り，『エウクレイデス全集』 斎藤憲・三浦伸夫／訳・解説 東京大学出版会で指摘されているようです。

グレブナー基底の力技で既約性判定

今日はネットで見かけた次の問題をグレブナー基底を使って力技で解いてみます。

は の元として既約である。

www1.ezbbs.net

ちなみに のグラフを描くと♡になります。

今回採用するのは因数分解の可能性を未定係数法でしらみつぶしに調べるというエレガントな解答からは程遠い方法ですが，グレブナー基底をコンピュータで計算していいなら意外とあっさり解くことができます。

イニシャル部分

多項式 の全次数が最高な単項式を拾って来たものをイニシャル部分と呼び と書くことにします。

例えば\begin{align}\mathrm{in}(x^3+2xy^2+xy+x+1)=x^3+2xy^2\end{align}です(全次数が3の部分)。

多項式 が \begin{align}f(x,y)=g(x,y)\times h(x,y)\end{align} と因数分解できたとすると，\begin{align}\mathrm{in}(f)=\mathrm{in}(g)\times \mathrm{in}(h)\end{align} が成り立ちます。

が既約だった場合， と のいずれかが定数になるので， と のいずれかが定数になります。よって が既約ならば も既約であることが分かります。

例えば とすると は で既約なので， も で既約であることが分かります。

の既約性

未定係数法

とすると となります。これは既約でないので，この時点では が既約かどうかわかりません。

さて，\begin{align}f(x,y)=g(x,y)\times h(x,y)\end{align}と定数でない の積に因数分解できたと仮定しましょう。

は定数でなく，積が になるので，あり得る可能性は定数倍と順番を除いて\begin{align}\mathrm{in}(g) =x^2+y^2,~~~\mathrm{in}(h)=(x^2+y^2)^2\end{align}しかありません。

実際にこれらをイニシャルに持つ が存在するか未定係数法で確かめてみましょう。
\begin{align}
h(x,y)&=x^2+y^2+a_1x+a_2y+a_3\\
g(x,y)&=(x^2+y^2)^2+b_1y^3+b_2xy^2+b_3x^2y+b_4x^3+b_5y^2+b_6xy+b_7x^2+b_8x+b_9y+b_{10}
\end{align}とおいて に現れる係数を全て列挙すると\begin{align}\small (*)
\begin{array}{l}
a_1+b_4, a_2+b_3, 2a_1+b_2+b_4, 2a_2+b_1+b_3+1, a_1+b_2, a_2+b_1, b_4a_1+a_3+b_7+3, \\
b_3a_1+b_4a_2+b_6, b_2a_1+b_3a_2+2a_3+b_5+b_7+6, b_1a_1+b_2a_2+b_6, b_1a_2+a_3+b_5+3, \\
b_7a_1+b_4a_3+b_8, b_6a_1+b_7a_2+b_3a_3+b_9, b_5a_1+b_6a_2+b_2a_3+b_8, b_5a_2+b_1a_3+b_9, \\
b_8a_1+b_7a_3+b_{10}-3, b_9a_1+b_8a_2+b_6a_3, b_9a_2+b_5a_3+b_{10}-3, b_{10}a_1+b_8a_3, b_{10}a_2+b_9a_3
\end{array}
\end{align}となります。つまりこれらが全て同時に となるような が存在するなら となるような が存在する事になって は可約，存在しないなら既約ということになります。これを手計算で確認するのはちょっと嫌ですよね。そこで登場するのがグレブナー基底です。

グレブナー基底

グレブナー基底は，とあるいい性質を持ったイデアルの生成系です。

グレブナー基底 - Wikipedia

詳しい定義や計算方法を知っていなくても以下の事実さえおさえていれば，とりあえずは大丈夫です。グレブナー基底はコンピュータが計算してくれます。

多項式の集合 の生成するイデアルのグレブナー基底が だったとすると，方程式系 \begin{align}p_1(x)=p_2=\dots=p_n(x)=0\end{align}と方程式系 \begin{align}q_1(x)=q_2(x)=\dots=q_m(x)=0\end{align}の解の集合は一致する。

とくに の生成するイデアルのグレブナー基底が となるとき，方程式 には解が存在しないので，方程式系 \begin{align}p_1(x)=p_2=\dots=p_n(x)=0\end{align}の解も存在しません。

既約性の証明

というわけで， に現れる係数を全て集めた が同時に全て になるかは，グレブナー基底を使ってテストすることができます。 が生成するイデアルのグレブナー基底を計算してみましょう。

sagecell.sagemath.org

S.<a_1,a_2,a_3,b_1,b_2,b_3,b_4,b_5,b_6,b_7,b_8,b_9,b_10> = PolynomialRing(QQ, 13, order='degrevlex')
J=ideal([a_1+b_4,a_2+b_3,2*a_1+b_2+b_4,2*a_2+b_1+b_3+1,a_1+b_2,a_2+b_1,b_4*a_1+a_3+b_7+3,b_3*a_1+b_4*a_2+b_6,b_2*a_1+b_3*a_2+2*a_3+b_5+b_7+6,b_1*a_1+b_2*a_2+b_6,b_1*a_2+a_3+b_5+3,b_7*a_1+b_4*a_3+b_8,b_6*a_1+b_7*a_2+b_3*a_3+b_9,b_5*a_1+b_6*a_2+b_2*a_3+b_8,b_5*a_2+b_1*a_3+b_9,b_8*a_1+b_7*a_3+b_10-3,b_9*a_1+b_8*a_2+b_6*a_3,b_9*a_2+b_5*a_3+b_10-3,b_10*a_1+b_8*a_3,b_10*a_2+b_9*a_3,b_10*a_3+1])
Gb=J.groebner_basis()
Gb

結果は次のようになります。

[1]

出力されたグレブナー基底は です。つまり， の係数が同時に全て になるような はありません。よって\begin{align}f(x,y)=(x^2+y^2-1)^3-x^2y^3\end{align}は で因数分解することはできず，既約であることが分かります。

離散フーリエ変換と中国剰余定理

今日紹介するのは離散フーリエ変換は中国剰余定理としても理解できるというお話です。この見方をすると，合成積が離散フーリエ変換で積に化ける理由がよく分かります。

離散フーリエ変換

を正整数とし， を の原始乗根をします。

長さ の複素数列 に \begin{align}A_p= \sum_{k=0}^{N-1} a_k \cdot \zeta_N^{-kp}\end{align}を対応させるものを離散フーリエ変換と呼び， で表します。

また， を \begin{align}a_p= \frac{1}{N}\sum_{k=0}^{N-1} A_k \cdot \zeta_N^{kp}\end{align}に対応させるものを逆離散フーリエ変換と呼び， で表します。

は線形同型写像で， が逆写像になっていることが知られています。つまり， のとき が成り立ちます。

離散フーリエ変換 - Wikipedia

離散フーリエ変換はフーリエ変換の離散版として，解析的な文脈で語られるのが普通ですが，今日は代数的な視点から見てみようと思います。

多項式環での中国剰余定理

複素数体 上の1変数多項式環 を で生成されるイデアル で割った剰余環を で表すことにします。 における中国剰余定理は次の形になります。

中国剰余定理
が \begin{align}f(T)=f_0(T)\cdots f_{N-1}(T)\end{align}と因数分解できており， はどの２つを取っても互いに素なとき，自然な全射 をまとめた写像\begin{align}\frac{\mathbb{C}[T]}{\langle f(T)\rangle}\to
\prod_{k=0}^{N-1} \frac{\mathbb{C}[T]}{\langle f_k(T)\rangle}\end{align}は -代数としての同型となる。

特に が相異なる複素数で，\begin{align}f(T)=\prod_{k=0}^{N-1} (T-a_k)\end{align}のときを考えると， であり， なので，この場合の中国剰余定理の同型写像は \begin{eqnarray*}\frac{\mathbb{C}[T]}{\langle \prod_{k=0}^{N-1} (T-a_k)\rangle} &\to&\mathbb{C}^N \cong \prod_{k=0}^{N-1} \frac{\mathbb{C}[T]}{\langle T-a_k\rangle}, \\[2mm]
g(T) &\mapsto& (g(a_0),~g(a_2),~\dots,~g(a_{N-1}))\end{eqnarray*}となります。

この同型により，任意の に対し，次数が高々 の多項式 で が成り立つものが唯一存在することが分かります。これを利用したのが最近一部ネットで話題の月の日数を与える多項式です。

togetter.com
tsujimotter.hatenablog.com

離散フーリエ変換と中国剰余定理

離散フーリエ変換の代数的解釈

の場合を考えましょう。 の逆数 も の原始乗根なので\begin{align}T^N-1=\prod_{k=0}^{N-1}(T-\zeta_N^{-k})\end{align}と因数分解できます。よって中国剰余定理より\begin{eqnarray*}\varphi:\frac{\mathbb{C}[T]}{\langle T^N-1\rangle} &\to&\mathbb{C}^N \\[2mm]
g(T) &\mapsto& (g(1),~g(\zeta_N^{-1}),~\dots,~g(\zeta_N^{-p}),\dots,~g(\zeta_N^{-(N-1)}))\end{eqnarray*}は環同型となります。

この定義域である環 は，ベクトル空間としては を基底とする 次元 -ベクトル空間です。この基底を並べたベクトルを とおいて， を の元 \begin{align}\vec{a}\cdot \vec{T}=a_0+a_1T+a_2T^2+\dots a_{N-1}T^{N-1}\end{align}と同一視することができます ( は内積)。

離散フーリエ変換の定義を思い出すと，\begin{align}\varphi(\vec{a}\cdot \vec{T})=\mathcal{F}(\vec{a})\end{align}が成り立つことが分かります。つまり， という同一視を通し，環同型 は離散フーリエ変換 そのものと思うことができます。

逆離散フーリエ変換の代数的解釈

は同型なので逆写像 が存在します。 がどうなるのか見てみましょう。

の標準的な基底を とします。 は 番目の成分が でそれ以外の成分が のベクトルです。

に対し \begin{align}\varphi\left(\frac{1}{N}\sum_{k=0}^{N-1} \zeta_N^{kp} T^k\right)=e_p\end{align}となります。 は -代数の準同型なので に対し \begin{eqnarray*}\varphi^{-1}(\vec{A})&=&\varphi^{-1}\left(\sum_{p=0}^{N-1} A_p e_p\right)=\sum_{p=0}^{N-1} A_p \varphi^{-1}(e_p) =\sum_{p=0}^{N-1}A_p\cdot\frac{1}{N}\sum_{k=0}^{N-1} \zeta_N^{kp} T^k\\
&=&\sum_{k=0}^{N-1}\left( \frac{1}{N}\sum_{\ell=0}^{N-1}A_p \zeta_N^{kp}\right)T^k=\mathcal{F}^{-1}(\vec{A})\cdot \vec{T}\end{eqnarray*}となり， は逆離散フーリエ変換と本質的に同じものであることが分かります。

合成積

さて は単なるベクトル空間としての同型ではなくて環同型です。 と の演算を比較すると，足し算はどちらもベクトルの足し算と同じ構造で似たようなものですが，掛け算の方はかなり違って見えます。

は環の直積なので積の構造は単純です。 の積は成分ごとの積と定義され\begin{align}(A_0,\dots,A_{N-1})(B_0,\dots,B_{N-1})=(A_0B_0,\dots, A_{N-1}B_{N-1})\end{align}となります。

一方で と の での積は\begin{align}f(T)g(T)=\sum_{k=0}^{N-1}\left(\sum_{p+q \equiv k ~\mathrm{mod}~ N} a_pb_q\right)T^k \end{align}となります。

ここで， の添え字を と解釈します。つまり，任意の整数 に対して です (数列 を周期 の繰り返しになるように添え字を 全体に拡張したと解釈してもいいです)。すると，先ほどの積は \begin{align}f(T)g(T)=\sum_{k=0}^{N-1}\left(\sum_{p=0}^{N-1} a_pb_{k-p}\right)T^k \end{align}と書けます。

この係数を並べたベクトルは合成積と呼ばれます。

合成積
， に対し， \begin{align}c_k=\sum_{p=0}^{N-1} a_pb_{k-p}\end{align} を と の合成積と呼び， と書く。

はベクトルの和を加法，合成積を乗法とした可換環になります。一見変わった環のような感じがしますが を考えていることと同じです。

中国剰余定理の同型 を使うと，合成積の離散フーリエ変換がどうなるかすぐ分かります。

合成積の離散フーリエ変換\begin{align}\mathcal{F}(\vec{a}*\vec{b})=\mathcal{F}(\vec{a})\mathcal{F}(\vec{b})\end{align}

ここで は直積環 での積です (つまり成分ごとに積を取る)。以前と同じように で，黒点 は内積の記号とします。

証明
合成積の定義より が で成り立つ。 は環準同型だったので， となる。

だったので，これは を意味している。

証明終