グレブナー基底の力技で既約性判定 - 現実と数学の区別が付かない

今日はネットで見かけた次の問題をグレブナー基底を使って力技で解いてみます。

$(x^2+y^2-1)^3-x^2y^3\in\mathbb{R}[x,y]$ は $\mathbb{R}[x,y]$ の元として既約である。

www1.ezbbs.net

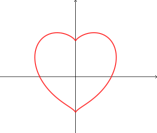
ちなみに $(x^2+y^2-1)^3-x^2y^3=0$ のグラフを描くと♡になります。

今回採用するのは因数分解の可能性を未定係数法でしらみつぶしに調べるというエレガントな解答からは程遠い方法ですが，グレブナー基底をコンピュータで計算していいなら意外とあっさり解くことができます。

イニシャル部分

多項式 $f(x,y)$ の全次数が最高な単項式を拾って来たものをイニシャル部分と呼び $\mathrm{in}(f)$ と書くことにします。

例えば\begin{align}\mathrm{in}(x^3+2xy^2+xy+x+1)=x^3+2xy^2\end{align}です(全次数が3の部分)。

多項式 $f(x,y)$ が \begin{align}f(x,y)=g(x,y)\times h(x,y)\end{align} と因数分解できたとすると，\begin{align}\mathrm{in}(f)=\mathrm{in}(g)\times \mathrm{in}(h)\end{align} が成り立ちます。

$\mathrm{in}(f)$ が既約だった場合， $\mathrm{in}(g)$ と $\mathrm{in}(h)$ のいずれかが定数になるので， $g$ と $h$ のいずれかが定数になります。よって $\mathrm{in}(f)$ が既約ならば $f(x,y)$ も既約であることが分かります。

例えば $f(x,y)=x^2+2y^2+y+2x+3$ とすると $\mathrm{in}(f)=x^2+2y^2$ は $\mathbb{R}[x,y]$ で既約なので， $f(x,y)$ も $\mathbb{R}[x,y]$ で既約であることが分かります。

$(x^2+y^2-1)^3-x^2y^3$ の既約性

未定係数法

$f(x,y)=(x^2+y^2-1)^3-x^2y^3$ とすると $\mathrm{in}(f)=(x^2+y^2)^3$ となります。これは既約でないので，この時点では $f(x,y)$ が既約かどうかわかりません。

さて，\begin{align}f(x,y)=g(x,y)\times h(x,y)\end{align}と定数でない $g(x,y),~h(x,y)\in \mathbb{R}[x,y]$ の積に因数分解できたと仮定しましょう。

$\mathrm{in}(g),~\mathrm{in}(h)$ は定数でなく，積が $\mathrm{in}(f)=(x^2+y^2)^3$ になるので，あり得る可能性は定数倍と順番を除いて\begin{align}\mathrm{in}(g) =x^2+y^2,~~~\mathrm{in}(h)=(x^2+y^2)^2\end{align}しかありません。

実際にこれらをイニシャルに持つ $g,~h$ が存在するか未定係数法で確かめてみましょう。
\begin{align}
h(x,y)&=x^2+y^2+a_1x+a_2y+a_3\\
g(x,y)&=(x^2+y^2)^2+b_1y^3+b_2xy^2+b_3x^2y+b_4x^3+b_5y^2+b_6xy+b_7x^2+b_8x+b_9y+b_{10}
\end{align}とおいて $h(x,y)\times g(x,y)-f(x,y)$ に現れる係数を全て列挙すると\begin{align}\small (*)
\begin{array}{l}
a_1+b_4, a_2+b_3, 2a_1+b_2+b_4, 2a_2+b_1+b_3+1, a_1+b_2, a_2+b_1, b_4a_1+a_3+b_7+3, \\
b_3a_1+b_4a_2+b_6, b_2a_1+b_3a_2+2a_3+b_5+b_7+6, b_1a_1+b_2a_2+b_6, b_1a_2+a_3+b_5+3, \\
b_7a_1+b_4a_3+b_8, b_6a_1+b_7a_2+b_3a_3+b_9, b_5a_1+b_6a_2+b_2a_3+b_8, b_5a_2+b_1a_3+b_9, \\
b_8a_1+b_7a_3+b_{10}-3, b_9a_1+b_8a_2+b_6a_3, b_9a_2+b_5a_3+b_{10}-3, b_{10}a_1+b_8a_3, b_{10}a_2+b_9a_3
\end{array}
\end{align}となります。つまりこれらが全て同時に $0$ となるような $a_i,~b_j\in\mathbb{R}$ が存在するなら $h(x,y)\times g(x,y)=f(x,y)$ となるような $a_i,~b_j\in\mathbb{R}$ が存在する事になって $f(x,y)$ は可約，存在しないなら既約ということになります。これを手計算で確認するのはちょっと嫌ですよね。そこで登場するのがグレブナー基底です。

グレブナー基底

グレブナー基底は，とあるいい性質を持ったイデアルの生成系です。

グレブナー基底 - Wikipedia

詳しい定義や計算方法を知っていなくても以下の事実さえおさえていれば，とりあえずは大丈夫です。グレブナー基底はコンピュータが計算してくれます。

多項式の集合 $\{p_1(x), \dots, p_n(x)\}\subset k[x_1,\dots,x_d]$ の生成するイデアルのグレブナー基底が $\{q_1(x),\dots, q_m(x)\}\subset k[x_1,\dots,x_d]$ だったとすると，方程式系 \begin{align}p_1(x)=p_2=\dots=p_n(x)=0\end{align}と方程式系 \begin{align}q_1(x)=q_2(x)=\dots=q_m(x)=0\end{align}の解の集合は一致する。

とくに $\{p_1(x), \dots, p_n(x)\}\subset k[x_1,\dots,x_d]$ の生成するイデアルのグレブナー基底が $\{1\}$ となるとき，方程式 $1=0$ には解が存在しないので，方程式系 \begin{align}p_1(x)=p_2=\dots=p_n(x)=0\end{align}の解も存在しません。

既約性の証明

というわけで， $h(x,y)\times g(x,y)-f(x,y)$ に現れる係数を全て集めた $(*)$ が同時に全て $0$ になるかは，グレブナー基底を使ってテストすることができます。 $(*)$ が生成するイデアルのグレブナー基底を計算してみましょう。

sagecell.sagemath.org

S.<a_1,a_2,a_3,b_1,b_2,b_3,b_4,b_5,b_6,b_7,b_8,b_9,b_10> = PolynomialRing(QQ, 13, order='degrevlex')
J=ideal([a_1+b_4,a_2+b_3,2*a_1+b_2+b_4,2*a_2+b_1+b_3+1,a_1+b_2,a_2+b_1,b_4*a_1+a_3+b_7+3,b_3*a_1+b_4*a_2+b_6,b_2*a_1+b_3*a_2+2*a_3+b_5+b_7+6,b_1*a_1+b_2*a_2+b_6,b_1*a_2+a_3+b_5+3,b_7*a_1+b_4*a_3+b_8,b_6*a_1+b_7*a_2+b_3*a_3+b_9,b_5*a_1+b_6*a_2+b_2*a_3+b_8,b_5*a_2+b_1*a_3+b_9,b_8*a_1+b_7*a_3+b_10-3,b_9*a_1+b_8*a_2+b_6*a_3,b_9*a_2+b_5*a_3+b_10-3,b_10*a_1+b_8*a_3,b_10*a_2+b_9*a_3,b_10*a_3+1])
Gb=J.groebner_basis()
Gb

結果は次のようになります。

[1]

出力されたグレブナー基底は $\{1\}$ です。つまり， $h(x,y)\times g(x,y)-f(x,y)$ の係数が同時に全て $0$ になるような $a_i,b_j$ はありません。よって\begin{align}f(x,y)=(x^2+y^2-1)^3-x^2y^3\end{align}は $\mathbb{R}[x,y]$ で因数分解することはできず，既約であることが分かります。